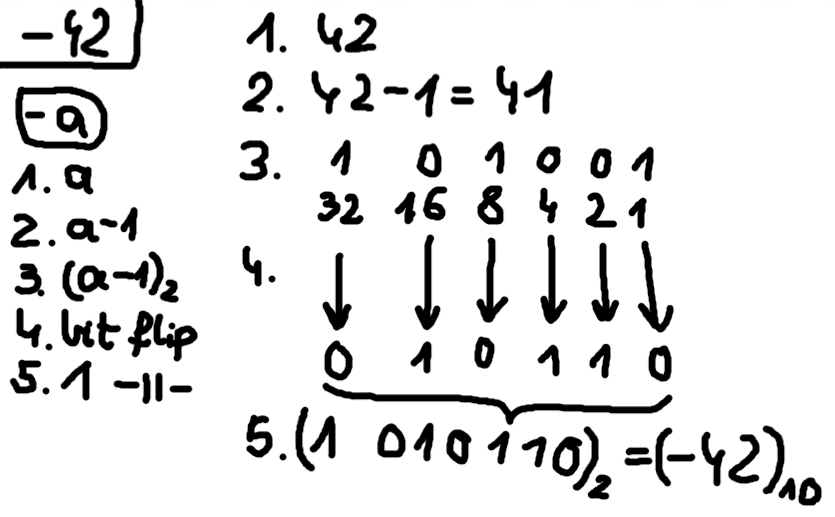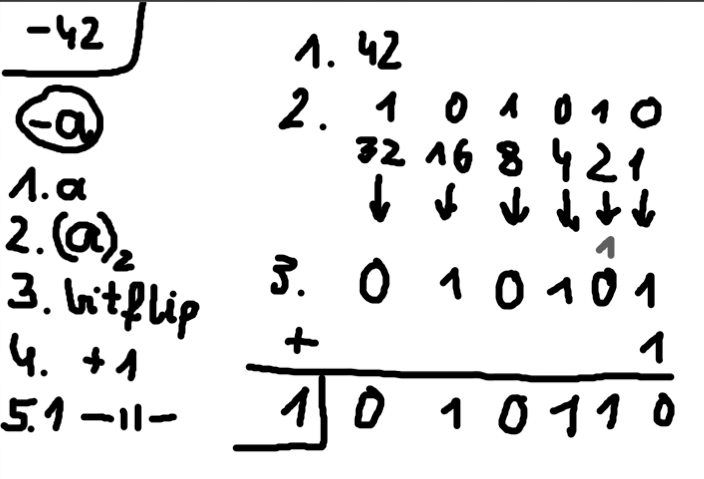Istnieją dwa sposoby na przedstawienie liczb binarnych:
- używając liczb niepodpisanych (unsigned int)
- używając liczb podpisanych (signed int)
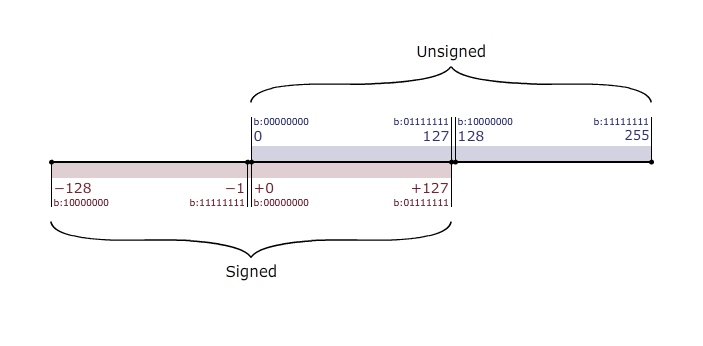
Liczby niepodpisane przyjmują wartości od 0 do \(2^{n}-1\), gdzie \(n\) to liczba bitów.
Łącznie \(n\) bitów jest w stanie zapisać \(2^n\) różnych wartości. Liczby niepodpisane nie przyjmują wartości ujemnych.
Liczba podpisana o n bitach może mieć wartość od \(-2^{n-1}\) do \(2^{n-1}-1\).
"Podpisanej" w liczbie podpisanej odnosi się do faktu, że pierwszy bit jest podpisany, czyli zawiera informację o tym, czy liczba jest dodatnia, czy też ujemna.
Łącznie \(n\) bitów może zapisać \(2^n\) różnych wartości (czyli tyle samo, co liczba niepodpisana).
W obu metodach zapisu różni się jedynie przedział liczb możliwych do zapisania: z użyciem liczb podpisanych możemy zapisywać wartości ujemne. Konsekwencją tego jest fakt, że nie możemy zapisać tak dużych liczb dodatnich, jak z użyciem liczb niepodpisanych. Poniżej zakres przedstawiony wizualnie:
Liczby binarne niepodpisane:
Do tej pory bazowaliśmy tylko na obliczaniu liczb binarnych niepodpisanych, dlatego nie będę tłumaczył tu jak się je konwertuje. Odsyłam do filmiku Mirosława Zelenta
Liczby binarne podpisane:
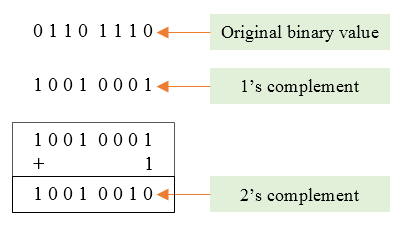
Poniżej będziemy używać kodu uzupełnień do dwóch (a nie sign-magnitude, ponieważ to drugie jest używane do przedstawiania ułamków w postaci binarnej, co mało nas interesuje).
Signed binary zestawienie liczb przy zerze:
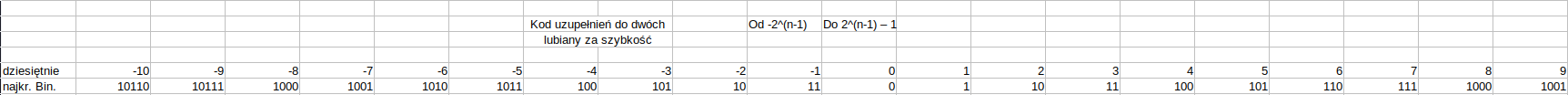
Używamy kodu uzupełnień do dwóch:
Sposób 1:
Sposób 2:
Tutaj lepiej zilustrowany sposób 2:
- Działania na podpisanych liczbach (nas obowiązuje tylko dodawanie)